Numbers Definition and 1000 Threads
-
M
Engineering Detector of even numbers in logic circuit
Homework Statement I need to make a circuit that detects even numbers. Need to find the equation for F when input A and B are both even. Input A: Word of 5 -bit signed representation in complement 2. Input B: Word of 3 -bit signed representation in complement 2. Homework Equations for B...- Max0007
- Thread
- Circuit Detector even Logic Numbers
- Replies: 24
- Forum: Engineering and Comp Sci Homework Help
-
E
What are the important numbers in Cosmology?
What are the important numbers in cosmology that dictates the very fate of the universe? I searched through Google and one site states that they are 13 constants; http://www.popularmechanics.com/flight/g163/13-most-important-numbers-in-the-universe/ What could be the possible consequences if... -
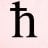
Why Can't Quantum Numbers Include Half Integers?
I don't understand why quantum numbers can not be divided into half integers and so on. The books I have read do not give clear explanations. Would anyone mind helping me understand this? Thanks!- HiggsBoson1
- Thread
- Numbers Quantum Quantum numbers
- Replies: 3
- Forum: Quantum Physics
-
C
Comparing 2-Bit Numbers with a Single Decoder and Standard Logic Gates
< Mentor Note -- thread moved to HH from the technical engineering forums, so no HH Template is shown >[/color] Is there a way to create two bit numbers comparator using one 2 to 4 decoder and standard logic gates?- cdummie
- Thread
- Bit Comparator Numbers
- Replies: 10
- Forum: Engineering and Comp Sci Homework Help
-

Do low atomic numbers not obey Moseley's law?
Helium has k-alpha of 24.5 eV whereas if we derive it using Moseley's law, then it is supposed to be 10.2 eV Also I then looked into many sources and found that Moseley's graph talks about elements having z>=10 only Later I found in few sources that the assumption that "one electron shields...- mukul
- Thread
- Atomic Law Numbers
- Replies: 1
- Forum: Quantum Physics
-
M
Question regarding complex numbers
1)If a= cosα + i sinα and the equation az2 + az +1 =0 has a pure imaginary root, then tanα=? 2) cosα+isinα=eiα , quadratic formula 3) What i tried to do was,i put a constant real number and tried to solve it and used demoivres theorem, although the answer is getting weirder and weirder.- Mohsin Hussain
- Thread
- Complex Complex numbers Numbers
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

Linear Algebra Linear algebra with complex numbers
Recommend a self study book for linear algebra with complex numbers- Ahmad Kishki
- Thread
- Algebra Complex Complex numbers Linear Linear algebra Numbers
- Replies: 2
- Forum: Science and Math Textbooks
-
E
Closed/Open Sets and Natural Numbers
Homework Statement I am trying to understand why ℕ the set of natural numbers is considered a Closed Set. 2. Relevant definition A Set S in Rm is closed iff its complement, Sc = Rm - S is open. The Attempt at a Solution I believe I understand why it is not an Open Set: Given that it...- emergentecon
- Thread
- Natural Natural numbers Numbers Set theory Sets
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
H
Principle and Angular Momentum Quantum Numbers
My understanding of the angular momentum quantum number is that a different number indicates a different region of space that the electron can occupy. So does the principle quantum number determine the size of that region? For example, is 2s the same as 3s in shape, but the 3s has a greater... -
X
MHB Solving 6-dimensional Equations | Find Unknown Numbers
How can the six unknown numbers be derived by constant letters of 6-dimensional equations?- xichyu1
- Thread
- Constant Numbers
- Replies: 1
- Forum: Differential Equations
-

Partial derivatives and complex numbers
Homework Statement show that the following functions are differentiable everywhere and then also find f'(z) and f''(z). (a) f(z) = iz + 2 so f(z) = ix -y +2 then u(x,y) = 2-y, v(x,y) = x Homework Equations z=x+iy z=u(x,y) +iv(x,y) Cauchy-Riemann conditions says is differentiable everywhere...- nmsurobert
- Thread
- Complex Complex numbers Derivatives Numbers Partial Partial derivatives
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
J
What does it mean to take positive rational numbers to whole
How do you do it- jim1174
- Thread
- Mean Numbers Positive Rational
- Replies: 3
- Forum: General Math
-

Expressing complex numbers in the x + iy form
Homework Statement ((1-i)/(sqrt2))^42 express in x+iy form Homework Equations z1/z1=(r1/r2)e^(i(theta1-theta2)) The Attempt at a Solution Ive found that (1-i) has r=sqrt2 so since r is sqrt2 and x=1 y=-1 so the angle is 7pi/4 so then I have (sqrt2e^(-i7pi/4)/sqrt2)^42 now from here is where I...- Logan Land
- Thread
- Complex Complex numbers Form Numbers
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-
G
Linking Fourier Transform, Vectors and Complex Numbers
Homework Statement Homework EquationsThe Attempt at a Solution I tried to attempt the question but I am not sure how to start it, at least for part (i). My biggest question, I think, is how does the multiplication of a random complex number to a Fourier-Transformed signal (V(f)) have an...- galaxy_twirl
- Thread
- Complex Complex numbers Electrical engineering Fourier Fourier transform Numbers Transform Vectors
- Replies: 8
- Forum: Engineering and Comp Sci Homework Help
-
B
Symbol in Alan Turing's On Computable Numbers
In Alan Turing's On Computable Numbers, he explains in his second paragraph the general notion of computable numbers. In doing so, he writes "In [symbol][symbol] 9, 10 I give some arguments...". I will include a screenshot of these symbols in this post. Do any of you know what these symbols...- Bluskyz
- Thread
- Computable Numbers Symbol Turing
- Replies: 2
- Forum: Computing and Technology
-

MHB Proving Inequality with Positive Real Numbers $x,\,y,\,z$
Let $x,\,y,\,z$ be positive real numbers such that $xy+yz+zx=3$. Prove the inequality $(x^3-x+5)(y^5-y^3+5)(z^7-z^5+5)\ge 125$.- anemone
- Thread
- Inequality Numbers Positive Real numbers
- Replies: 1
- Forum: General Math
-
M
Sum of n consecutive numbers is divisible by n
I'm trying to investigate this statement: The sum of n consecutive numbers is always divisible by n. I've found already that it's only true when the total amount of numbers is an odd number. I've also found that the median and mean are the same with consecutive numbers. I can not prove that the...- Matt
- Thread
- Numbers Sum
- Replies: 9
- Forum: General Math
-

MHB Every interval (a,b) contains both rational and irrational numbers
I am reading Chapter 1:"Real Numbers" of Charles Chapman Pugh's book "Real Mathematical Analysis. I need help with the proof of Theorem 7 on pages 19-20. Theorem 7 (Chapter 1) reads as follows: In the above proof, Pugh writes: " ... ... The fact that $$a \lt b$$ implies the set B \ A...- Math Amateur
- Thread
- Interval Irrational Irrational numbers Numbers Rational
- Replies: 2
- Forum: Topology and Analysis
-

How Do Numbers Shape Our Everyday Lives?
Radiolab is a radio show broadcast on public radio stations across the United States. This week's Radiolab was titled Numbers. This Numbers podcast discusses how numbers affect our daily lives, how infants intuitively perceive numbers (logarithmically), and how children eventually learn to...- collinsmark
- Thread
- Numbers
- Replies: 1
- Forum: General Discussion
-

MHB What is the definition of real numbers in terms of rational sequences?
Hi! (Smile) We define the set $U=\mathbb{Z} \times (\mathbb{Z}-\{0\})$ and over $U$ we define the following relation $S$: $$\langle i,j \rangle S \langle k,l \rangle \iff i \cdot l=j \cdot k$$ $$\mathbb{Q}=U/S=\{ [\langle i, j \rangle ]_S: i \in \mathbb{Z}, j \in \mathbb{Z} \setminus \{0\}...- evinda
- Thread
- Numbers Real numbers
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
A
How many numbers that are multiples of 5 divide 1000?
Homework Statement Okay: How many numbers divide 1000 that are multiples of 5 I have seen you do 1000/5 = 200 But how does this mean there are 200 numbers that divide 1000 that are multiples of 5? This just says: 1000 divided into 5 equal pieces, is 200. So how does this give how many...- Amad27
- Thread
- Number theory Numbers
- Replies: 24
- Forum: Precalculus Mathematics Homework Help
-

MHB Can Recursion Define Natural Number Addition?
Hello! (Wave) For each pair of natural numbers $m \in \omega, n \in \omega$ we define: $$m+0=m\\m+n'=(m+n)'$$ We fix a $m$ and recursively the operation $m+n$ is defined for any $n \in \omega$. Knowing for example that $m+0=m$ we can conclude what $m+1$ means. $$m+1=m+0'=(m+0)'=m'$$ and...- evinda
- Thread
- Natural Natural numbers Numbers Properties
- Replies: 16
- Forum: Set Theory, Logic, Probability, Statistics
-

Complex numbers and differential equations for physics
How relevant is complex analysis to physics? I really want to take differential equations but I would have to change my schedule around way more than I want to. So, would anyone advise a physics major to to take complex analysis? Should I just change my schedule around so I can take differential...- neosoul
- Thread
- Complex Complex analysis Complex numbers Differential Differential equations Numbers Physics
- Replies: 2
- Forum: STEM Academic Advising
-
P
Why were complex numbers introduced in physics?
hello can you tell me please why we introduced complex numbers? what was the problem that we couldn't express with rest of algebra and we introduced complex numbers? I am basically interested in why we introduced complex number to describe and analyze AC circuits, like voltage, current and...- physior
- Thread
- Complex Complex numbers Numbers Physics
- Replies: 32
- Forum: Other Physics Topics
-
M
Understanding the Solution for Finding the Sum of Digits of m
Homework Statement Let m be the number of numbers fromantic the set {1,2,3,...,2014} which can be expressed as difference of squares of two non negative integers. The sum of the digits of m is ... Homework EquationsThe Attempt at a Solution I got a solution from a magazine but I didn't under...- Murtuza Tipu
- Thread
- Explain Number theory Numbers Square
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

MHB Prove Natural Numbers Subset Property
Hello! (Wave) I want to prove that for any natural numbers $n,m$ it holds that: $$n \subset m \leftrightarrow n \in m \lor n=m$$ $"\Leftarrow"$: Using the sentence: "For any natural numbers $m,n$ it holds that $n \in m \rightarrow n \subset m$" if $n \in m \lor n=m$, we conclude that $n...- evinda
- Thread
- Natural Natural numbers Numbers
- Replies: 30
- Forum: Set Theory, Logic, Probability, Statistics
-

Qubits, 2 complex numbers, forcing one to real
Hi All, I'm working out a program to emulate a quantum computer (definitely in a nascent stage), and I'm struggling with a piece of the math. I looked at the math sections in these forums, but thought this might be more appropriate to post it. I'll try to conceptually outline the problem, and...- Elroy
- Thread
- Complex Complex numbers Numbers Qubits
- Replies: 5
- Forum: Quantum Physics
-
T
Learning General Relativity: Finding Examples with Numbers
I am currently learning general relativity and I kind of understand what the symbols in einstein field equationd represent. But I need example like those that involves actual numerical values. I have been trying to search for it online but I cant. So does anyone mind showing me how you apply...- TimeRip496
- Thread
- General General relativity Numbers Relativity
- Replies: 2
- Forum: Special and General Relativity
-
E
Rotation formula Complex numbers
Homework Statement If arg(\frac{z-ω}{z-ω^2}) = 0, \ then\ prove \ that\ Re(z) = -1/2 Homework Equations ω and ω^2 are non-real cube roots of unity. The Attempt at a Solution arg(z-ω) = arg(z-ω^2) So, z-ω = k(z-w^2) Beyond that, I'm not sure how to proceed. Using the rotation formula may also...- erisedk
- Thread
- Complex Complex numbers Formula Numbers Rotation
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
G
Feynman rules - where do the imaginary numbers come from?
I'm trying to learn how to derive Feynman rules (what else to do during xmas, lol). The book I'm using is QFT 2nd ed by Mandl&Shaw. On p 428 they're trying to show how to derive a Feynman rule for W W^\dagger Z^2 interaction term g^2 \cos^2\theta_W\left[W_\alpha W_\beta^\dagger Z^\alpha Z^\beta...- guest1234
- Thread
- Feynman Feynman rules Imaginary Imaginary numbers Numbers Rules
- Replies: 3
- Forum: Quantum Physics
-
P
MHB Determining the Median of Five Median Numbers
Problem: My goal is to show the median income among five different groups of people, where the median income for each group has already been determined. Is it as simple as choosing the median income of $ 45,615 since there are five numbers? Here is the information: Group One's Median Income...- Patty Kirk
- Thread
- Median Numbers
- Replies: 1
- Forum: General Math
-
B
Multiplying numbers from One set with another set
Homework Statement Bob makes two sets: one with all the even integers between 1 and 30 inclusive, and another with all the odd integers inclusive. He called the sets Q and R. He multiplied each number from Q with each number in R. Then he added the 225 products together and called the result...- brisk11228
- Thread
- Numbers Set
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
L
What makes complex numbers so special?
Is there in a nutshell an explanation or even a single reason why complex numbers have so many fascinating consequences and give rise to so much deep stuff like analytic functions (with all its stunning properties), Riemann surfaces, analytic continuations, modular forms, zeta function, its...- Lapidus
- Thread
- Complex Complex numbers Numbers
- Replies: 4
- Forum: General Math
-
P
Why is the principal square root of a complex number not well-defined?
Within the context of real numbers, the square root function is well-defined; that is, the function ##f## defined by: ##f(x) = \sqrt{x}## Refers to the principal root of any real number x. Is it true that this is not the case when dealing with complex numbers? Does ##\sqrt{z}##, where ##z ∈ ℂ##...- PFuser1232
- Thread
- Complex Complex numbers Numbers Roots
- Replies: 2
- Forum: General Math
-
J
What is the easiest method for adding and subtracting rational numbers
What is the easiest method for adding and subtracting rational numbers- jim1174
- Thread
- Method Numbers Rational Subtracting
- Replies: 5
- Forum: General Math
-
O
Possible combinations of numbers?
Homework Statement Assuming 10 people pick a number between 1-120 and no two numbers can be the same, how many combinations of numbers can their be?Homework Equations C=N^s The Attempt at a Solution So I know the total possible for 120 would be just 120^10, but if I want to solve for the...- orangeincup
- Thread
- Combinations Numbers
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

MHB Find the number of real numbers that satisfy the given equation
How many real numbers $x$ satisfy $\sin x=\dfrac{x}{100}$?- anemone
- Thread
- Numbers Real numbers
- Replies: 7
- Forum: General Math
-

How many 7-digit numbers are divisible by 7 and composed of digits 1-7?
Submitted by @PeroK Consider all 7-digit numbers which are a permutation of the digits 1-7. How many of these are divisible by 7? Can you prove the answer algebraically, rather than simply counting them? Please make use of the spoiler tag- Greg Bernhardt
- Thread
- Challenge Numbers
- Replies: 4
- Forum: General Math
-
B
MHB Can a Natural Number Satisfy n ≡ 1 (mod p) for All Primes in a Large Set?
Let $\left\{ p_{1},p_{2},\dots,p_{h}\right\}$ a set of consecutive prime numbers. I want to show that, if $h$ is large enough, then doesn't exists a natural number $n$ such that $$n\equiv1\textrm{ mod }p_{i},\,\forall i=1,\dots,h.$$ I think is true but I have no idea how to prove it. Am I wrong?- Bibubo
- Thread
- Class Numbers
- Replies: 1
- Forum: General Math
-

How to find min and max of 100 numbers ?
Homework Statement The minimum number of comparisons required to find the minimum and the maximum of 100 numbers is ... Homework Equations ##T(n)=T(\lceil \frac{n}{2} \rceil) + T(\lfloor \frac{n}{2} \rfloor) + 2## The Attempt at a Solution Recurrence for the above problem is ##T(n)=T(\lceil...- 22990atinesh
- Thread
- Algorithm Max Numbers
- Replies: 1
- Forum: Engineering and Comp Sci Homework Help
-

MHB Square Numbers Satisfying $3x^2+x=4y^2+y$
show that for x,y positive integers satisfying $3x^2+x= 4y^2+y$ each of x-y , 3x+3y+ 1 and 4x + 4y + 1 are squares. ( above equation has atleast one solution x= 30 and y = 26)- kaliprasad
- Thread
- Numbers Square
- Replies: 4
- Forum: General Math
-
I
Systems of Equations with Complex Numbers
Mod note: This thread was moved from a technical math section, so doesn't include the homework template. I know this has been asked before, but none of the other posts have helped me. I cannot for the life of me figure out how to solve a system of equations with complex numbers. Here is a very...- inshooter
- Thread
- Complex Complex numbers Numbers Systems Systems of equations
- Replies: 13
- Forum: Precalculus Mathematics Homework Help
-
N
N00b question about understanding what formulas are
I am new to the world of Science & Mathematics but am eager to learn all I can. I go to my local library and open up books on the topic such as Physics, Engineering and Electronics and there are swathes of formulas all of which I don't understand. I stare at them wondering what keys they must...- Niaboc67
- Thread
- Formulas Numbers Physics Variables
- Replies: 7
- Forum: Other Physics Topics
-
B
Gaps In The System of Rational Numbers
I have a question which comes from Rudin's Principles of Mathematical Analysis; specifically, from the introduction. In example 1.1, the author clearly shows that no rational numbers satisfy the equation ##p^2 = 2##. So, I am trying to imagine myself in a scenario in which I am in a time before...- Bashyboy
- Thread
- Numbers Rational System
- Replies: 29
- Forum: General Math
-
X
Natural numbers distributive lattice
I need a proof that the set of natural numbers with the the relationship of divisibility form a distributive lattice with gcd as AND and lcm as OR. I know it can be shown that a AND (b OR c) >= (a AND b) OR (a AND c) for a general lattice, and that if we can show the opposite, that a AND (b OR...- Xael
- Thread
- Lattice Natural Natural numbers Numbers
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-

Comp Sci Fortran90: DO loop for sequence of numbers
Homework Statement A program finds the area under the Gaussian Distribution Curve between ±σ using Simpsons Rule. Modify the program to investigate the effect of the number of strips. Do this by using a DO loop in the main program for the following sequence of number of strips (n); n-2, n-4...- SalfordPhysics
- Thread
- Area Fortran Fortran90 Integration Loop Numbers Numerical methods Programming Sequence
- Replies: 4
- Forum: Engineering and Comp Sci Homework Help
-

MHB Harmonic Numbers Identity Proof?
Prove the following $$\sum_{k=1}^n \frac{H_k}{k} = \frac{H_n^2+H^{(2)}_n}{2}$$ where we define $$H^{(k)}_n = \sum_{j=1}^n \frac{1}{j^k} \,\,\, ; \,\,\, H^2_n = \left( \sum_{j=1}^n \frac{1}{j}\right)^2 $$- alyafey22
- Thread
- Harmonic Identity Numbers
- Replies: 3
- Forum: General Math
-
I
Finding at which point multiplied numbers coalesce
Hello! This is not really a homework question, more of a question of what I should do for "homework", but I hope it is acceptable. My question is regarding a method of finding at which point (if at all) two different numbers, when multiplied, reach the same number. For example, how could I...- ignorant2
- Thread
- Numbers Point
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
H
Complex numbers: Find the Geometric image
Homework Statement Find the Geometric image of; 1. ## | z - 2 | - | z + 2| < 2; ## 2. ## 0 < Re(iz) < 1 ## Homework EquationsThe Attempt at a Solution In both cases i really am struggling to begin these questions, complex numbers are not my best field. There are problems before this one...- HMPARTICLE
- Thread
- Complex Complex numbers Geometric Image Numbers
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
H
Complex numbers and completing the square
Homework Statement let z' = (a,b), find z in C such that z^2 = z' Homework EquationsThe Attempt at a Solution let z = (x,y) then z^2 = (x^2-y^2, 2xy) since z^2 = z', we have, (x^2-y^2, 2xy) = (a,b) comparing real and imaginary components we have; x^2-y^2 = a, 2xy = b. Now, this...- HMPARTICLE
- Thread
- Complex Complex numbers Numbers Square
- Replies: 6
- Forum: Calculus and Beyond Homework Help