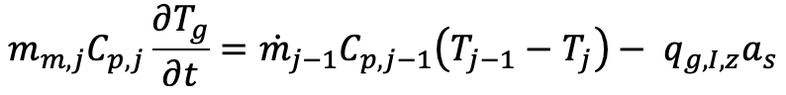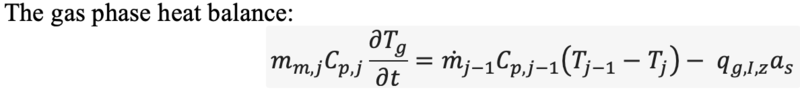Modelling of two phase flow in packed bed (continued)

[casualguitar]

Mass Transfer Rate for Deposition of CO2 and Water

The following is still somewhat approximate, but is a significant improvement to the mass transfer rate approach used by Tuinier et al:
$$\dot{M}_i^"=k_i\left(\frac{Py_i-p_i(T_I)}{RT_I}\right)\tag{1}$$where $\dot{M}_i^"$ is the molar flux of species per unit area of surface, P is the total pressure, $y_i$ is the mole fraction of species in the bulk gas, $p_i(T_I)$ is the equilibrium vapor pressure of species at the interface temperature $T_I$, and $k_i$ is the mass transfer coefficient (units of m/s) of species for deposition from the gas.

Ok then similar to the Tuinier et al model you're saying that mass transfer rate will be proportional to the difference between the partial pressure of the species and the equilibrium vapour pressure of the species

Where does equation 1 come from? Is this an equation you derived or is it an established equation?

The mass transfer coefficient ki is related to the local Sherwood number for mass transfer by Shloc,i=kiDp(1−ϵg)Diψwhere Di is the diffusion coefficient of species in N2 and ψ is the packing particle shape factor (equal to 1.0 for spherical particles and 0.92 for cylindrical particles).

Got it, so I guess we will be able to find Sherwood number correlations for packed beds in Bird et al that we can use here to solve for the mass transfer coefficient

By Reynolds analogy, the Sherwood number Shloc,i is the same function of Reynold number and Schmidt number as the Nussult number is as a function of Reynolds number and Prantdl number, respectively.

So if the Nusselts number tells you how convection or conduction dominant the heat transfer is, the Sherwood number tells you how convection or diffusion dominant the mass transfer is?

An additional constraint on Eqn. 1 is that M˙i" must be zero if the number of moles of deposit per unit area of surface is zero and the right hand side of Eqn. 1 is negative. This means that the number of moles per unit area of deposit on the surface of the particles can never go negative.

Got it

This just leaves us with the $U_g$ and $U_b$ correlations then? On this now

 

[Chestermiller]

Ok then similar to the Tuinier et al model you're saying that mass transfer rate will be proportional to the difference between the partial pressure of the species and the equilibrium vapour pressure of the species

Where does equation 1 come from? Is this an equation you derived or is it an established equation?

It is an established equation using the mass transfer coefficient analogous to the heat transfer coefficient. See chapters 17 and forward in BSL, Treybel (Mass Transfer Operations), and Chemical Engineers' Handbook

Got it, so I guess we will be able to find Sherwood number correlations for packed beds in Bird et al that we can use here to solve for the mass transfer coefficient

Like I said, you use the same BSL correlation for Sh in terms of Re and Sc that you use for heat transfer Nu in terms of Re and Pr.

So if the Nusselts number tells you how convection or conduction dominant the heat transfer is, the Sherwood number tells you how convection or diffusion dominant the mass transfer is?

Nu is for convective heat transfer and Sh is for convective mass transfer.

Got it

This just leaves us with the $U_g$ and $U_b$ correlations then? On this now

I recommend using the same BSL correlations that we used in the other model.

 

[casualguitar]

Like I said, you use the same BSL correlation for Sh in terms of Re and Sc that you use for heat transfer Nu in terms of Re and Pr.

Got it, I found where it does that in BSL also

I recommend using the same BSL correlations that we used in the other model.

Ok interesting so this flow as done in the previous model:

applies for both $U_g$ and $U_b$ (using the relevant solid and fluid parameters for $U_b$ and $U_g$ respectively). We can also swap out the Prandtl number for the Schmidt number and then this flow applies for the mass transfer coefficient $k_i$ also? If so this makes the coding efficient

Where $Sc = \frac{\mu}{\rho D}$. The equivalent $k_g$ term from model 1 was found via the thermo library assuming $k_g$ was temperature and pressure dependent. I don't think thermo will give the mass diffusivity so we will need a correlation for $D$ here also. I guess BSL will have this?

Note:
Just looking at the correlation used for $U$ in the previous model, its not clear to me how to apply this separately to $U_g$ and $U_b$ in this model. It seems that we will only need to use the fact that $T_g$ does not equal $T_b$. Is it correct to say that the only difference between the $U_g$ and $U_b$ models is that the $U_g$ parameters are evaluated at $T_g$ and the $U_b$ parameters are evaluated at $T_b$?

Or if the above is not correct then maybe we should go with the approach below (outlined in BSL ch.14) where you take the average temperature so $U_b$ parameters would be evaluated at $\frac{(TI+TB)}{2}$ and $U_g$ parameters at $\frac{(TI+TG)}{2}$?

 

[casualguitar]

It is an established equation using the mass transfer coefficient analogous to the heat transfer coefficient. See chapters 17 and forward in BSL, Treybel (Mass Transfer Operations), and Chemical Engineers' Handbook

Like I said, you use the same BSL correlation for Sh in terms of Re and Sc that you use for heat transfer Nu in terms of Re and Pr.

Nu is for convective heat transfer and Sh is for convective mass transfer.

I recommend using the same BSL correlations that we used in the other model.

Just one other question - I'll be using the previous HTC functions I made for this (plus a new one for the Sc number). I think there is a bug in one of my functions though. Do you know what the typical ranges for the Pr, Re, Nu, Sc numbers and U in the previous model (model 1) would be? Just to help with the debug!

Also I believe you previously commented on my sleeping patterns (early on in model 1). I see you're also awake at a quite early time of 4am! An early bird or a late night owl?

Edit:
Lastly, we had the lumping of the convective and conductive terms in the last model for U:

Does the same lumping apply for the convective and diffusive mass transfer? Meaning that we would get something like:
$$k_i = \frac{1}{\frac{1}{k_{fs}} + \frac{dp/\beta}{D}}$$

 

[Chestermiller]

Got it, I found where it does that in BSL also

Ok interesting so this flow as done in the previous model:
View attachment 299928
applies for both $U_g$ and $U_b$ (using the relevant solid and fluid parameters for $U_b$ and $U_g$ respectively). We can also swap out the Prandtl number for the Schmidt number and then this flow applies for the mass transfer coefficient $k_i$ also? If so this makes the coding efficient

I can't read your handwriting again. Please use Latex or provide a post # from the previous thread.

Where $Sc = \frac{\mu}{\rho D}$. The equivalent $k_g$ term from model 1 was found via the thermo library assuming $k_g$ was temperature and pressure dependent. I don't think thermo will give the mass diffusivity so we will need a correlation for $D$ here also. I guess BSL will have this?

Just google "diffusivity of CO2 (and H2O)" in Nitrogen. That should be good enough. BSL will have H2O probably.

Note:
Just looking at the correlation used for $U$ in the previous model, its not clear to me how to apply this separately to $U_g$ and $U_b$ in this model. It seems that we will only need to use the fact that $T_g$ does not equal $T_b$. Is it correct to say that the only difference between the $U_g$ and $U_b$ models is that the $U_g$ parameters are evaluated at $T_g$ and the $U_b$ parameters are evaluated at $T_b$?

This is not going to be exact. I would use T at the interface.

Or if the above is not correct then maybe we should go with the approach below (outlined in BSL ch.14) where you take the average temperature so $U_b$ parameters would be evaluated at $\frac{(TI+TB)}{2}$ and $U_g$ parameters at $\frac{(TI+TG)}{2}$?

View attachment 299929

This would be adequate too. Like I said, it won't be exact. This is a judgment call.

 

[Chestermiller]

Just one other question - I'll be using the previous HTC functions I made for this (plus a new one for the Sc number). I think there is a bug in one of my functions though. Do you know what the typical ranges for the Pr, Re, Nu, Sc numbers and U in the previous model (model 1) would be? Just to help with the debug!

This is why I suggested in the previous model that you compare the two gas phase correlations given in BSL and your other reference.

Also I believe you previously commented on my sleeping patterns (early on in model 1). I see you're also awake at a quite early time of 4am! An early bird or a late night owl?

My dog was barking, and he pooped on the kitchen floor before I could get him outside.

Edit:
Lastly, we had the lumping of the convective and conductive terms in the last model for U:
View attachment 299934
Does the same lumping apply for the convective and diffusive mass transfer? Meaning that we would get something like:
$$k_i = \frac{1}{\frac{1}{k_{fs}} + \frac{dp/\beta}{D}}$$

No. There is no diffusion in the solid bed particles. You just use the mass transfer coefficient for the gas phase. The mass transfer model just applies from the bulk gas to the solidification interface.

 

[casualguitar]

Just google "diffusivity of CO2 (and H2O)" in Nitrogen. That should be good enough. BSL will have H2O probably.

Are we looking for a correlation here or assuming a constant?

This is not going to be exact. I would use T at the interface.

This would be adequate too. Like I said, it won't be exact. This is a judgment call.

It will be a small code change to switch between these so that can be decided later

I can't read your handwriting again. Please use Latex or provide a post # from the previous thread.

So this is the model I would be using (same as model 1) to calculate $U_g$ and $U_b$. $U_g$ is evaluated using $\frac{(TI+TG)}{2}$ and $U_B$ using $\frac{(TI+TB)}{2}$. You suggested earlier using $T_I$ for both. Would this not mean that $U_g$ would be equal to $U_b$ always?

 

[casualguitar]

This is why I suggested in the previous model that you compare the two gas phase correlations given in BSL and your other reference.

Would you know the expected order for these parameters (Re, Pr, Nu, U)?

My dog was barking, and he pooped on the kitchen floor before I could get him outside.

Ideal start to the day!

 

[casualguitar]

No. There is no diffusion in the solid bed particles. You just use the mass transfer coefficient for the gas phase. The mass transfer model just applies from the bulk gas to the solidification interface.

I think I understand. So the mass and heat transfer models are equivalent, except we leave out the final 'lumping' equation as we had in the heat transfer model? Leaving us with this mass transfer model:

Seem reasonable to you?

 

[Chestermiller]

I think I understand. So the mass and heat transfer models are equivalent, except we leave out the final 'lumping' equation as we had in the heat transfer model? Leaving us with this mass transfer model:
View attachment 299937
Seem reasonable to you?

No. $$Sh_{loc,i}=(2.19 Re^{\frac{1}{3}}+0.78 Re^{0.619})Sc^{\frac{1}{3}}$$

 

[casualguitar]

No. $$Sh_{loc,i}=(2.19 Re^{\frac{1}{3}}+0.78 Re^{0.619})Sc^{\frac{1}{3}}$$

Whoops yes I got that result also

The last bit seems to be the diffusivity of both CO2 and H2O in N2. A constant value or a temperature dependent correlation? I can find approximate constant values easily (approx 0.22cm2/s and 0.15 cm2/s for water and CO2, both at 273K). There seems to be a lot of literature on this though so correlations should be available

One question - how does this model deal with liquid phase water?
Looking at the heat balances and this equation

there seems to be no reason why we couldn't swap out the heat of fusion for the heat of vaporisation here as required.

However for the mass balances we don't seem to have a way to track the amount of liquid present, only solid deposition, so my thought is that this model effectively assumes that water moves from gas phase to solid phase and back very quickly i.e. fast enough to assume no liquid phase is present? Is this the assumption being made in Tuinier et al also?

Besides those correlations to be found, it looks like the computational flow is the next point?

Hmm I don't understand at what point we can actually solve for the $q$ values

Similar to the last model we know $\dot{m}_0$ into the bed so we can solve the gas phase mole balance immediately I think. To solve for the $q$ values we need $T_g$ and $T_b$ which we don't have yet, so my guess is that the gas and bed heat balances must be solved simultaneously? Then we can also solve the solid phase mass balance once we have these temperatures and the interface temperature

Once we have $T_g$ and $T_b$ we can solve for the mass flow out of a tank. This cycle then repeats for the other beds

 

[Chestermiller]

Whoops yes I got that result also

The last bit seems to be the diffusivity of both CO2 and H2O in N2. A constant value or a temperature dependent correlation? I can find approximate constant values easily (approx 0.22cm2/s and 0.15 cm2/s for water and CO2, both at 273K). There seems to be a lot of literature on this though so correlations should be available

See Chapter 17 of BSL.

One question - how does this model deal with liquid phase water?
Looking at the heat balances and this equation
View attachment 300047
there seems to be no reason why we couldn't swap out the heat of fusion for the heat of vaporisation here as required.

However for the mass balances we don't seem to have a way to track the amount of liquid present, only solid deposition, so my thought is that this model effectively assumes that water moves from gas phase to solid phase and back very quickly i.e. fast enough to assume no liquid phase is present? Is this the assumption being made in Tuinier et al also?

This is a bit of a dilemma. Tuinier are assuming that water deposits as liquid and CO2 deposits as solid. But there is no allowance for the conversion of deposited liquid water to deposited ice in their approach, even if they did switch from the liquid to the solid vapor pressure curve to describe the behavior during the deposition. The heat of vaporization of water is >540 cal/gm, and the heat of fusion of water is 80 cal/gm, so it may not matter much. They may be using a single value for the heat of phase change of water and a single value for CO2, irrespective of temperature. This neglects:
1. Changes is heat of sublimation or vaporization with temperature
2. Heat of fusion of water
3. Changes in sensible heat of deposits.
4. The deposition processes of H20 and CO2 do not interact
This seems to be the approximation they are using in this model, and it may be a pretty good approximation, in view of other approximations that are inherent in the model.

Besides those correlations to be found, it looks like the computational flow is the next point?

View attachment 300048
Hmm I don't understand at what point we can actually solve for the $q$ values

These are expressed in terms of the deposition rates, heats of deposition, bulk temperature of the bed and gas, and heat transfer coefficients by the equations I gave.

Similar to the last model we know $\dot{m}_0$ into the bed so we can solve the gas phase mole balance immediately I think. To solve for the $q$ values we need $T_g$ and $T_b$ which we don't have yet, so my guess is that the gas and bed heat balances must be solved simultaneously? Then we can also solve the solid phase mass balance once we have these temperatures and the interface temperature

Once we have $T_g$ and $T_b$ we can solve for the mass flow out of a tank. This cycle then repeats for the other beds

This looks OK. I recommend doing each tank in sequence at a given time step using Crank-Nicholson type approximation.

 

[casualguitar]

These are expressed in terms of the deposition rates, heats of deposition, bulk temperature of the bed and gas, and heat transfer coefficients by the equations I gave.

Yes however I'm not sure yet if they are solved at each position/time step independently of the ODEs they are part of i.e. do we solve for the q values first and then use these values in solving the relevant ODEs, or are the q values solved for at the same time as the ODE is being solved (simultaneously)

I recommend doing each tank in sequence at a given time step using Crank-Nicholson type approximation.

Previously we used the available integrators (ODEint and solve_ivp). Neither of these have a CN approximation available. Are you suggesting hard coding the CN solution, rather than using an integrator library? I have no issue with that the learning might be good. Is there any advantage to hard coding rather than using an available integrator here?

 

[Chestermiller]

Yes however I'm not sure yet if they are solved at each position/time step independently of the ODEs they are part of i.e. do we solve for the q values first and then use these values in solving the relevant ODEs, or are the q values solved for at the same time as the ODE is being solved (simultaneously)

No. The expressions for the q's are substituted into the two respective heat transfer differential equations.

Previously we used the available integrators (ODEint and solve_ivp). Neither of these have a CN approximation available. Are you suggesting hard coding the CN solution, rather than using an integrator library?

Sure. That's not a problem right? I'm suggesting solving them for each tank at each time step using predictor-corrector.

I have no issue with that the learning might be good. Is there any advantage to hard coding rather than using an available integrator here?

The available integrators won't do one tank at a time in sequence.

 

[casualguitar]

No. The expressions for the q's are substituted into the two respective heat transfer differential equations.

Got it

Sure. That's not a problem right? I'm suggesting solving them for each tank at each time step using predictor-corrector.

No problem with that. I actually prefer the idea of doing this manually because I think it would be beneficial/interesting to see exactly what's going on (the integrator libraries sort of hide this). It is also what my own supervisor suggested for the previous model (before I used an integrator library)

I'm suggesting solving them for each tank at each time step using predictor-corrector.

Ok. I have never coded something like this manually. I have seen examples of CN being implemented in python though so I can follow these

The available integrators won't do one tank at a time in sequence.

Is this not what we did in the previous model? Solve for all values across all tanks at a single time before continuing to the next time step?

Lastly, if the available integrators won't do one tank at a time in sequence, why choose this approach? What is the advantage of this?

To be clearer on the above question, I'm asking -
Why did we use an integrator for the previous model rather than manually code it, and why is this approach not being used this time around. i.e. what is different between the two models that it is better to manually code CN this time?

Will do a final collation of the equations/correlations this evening and then start the CN solution tomorrow. I think for now I'll assume a constant value for everything I reasonably can i.e. just focus on getting actual solutions to the differential equations without worrying about correlations etc being used right also

 

[Chestermiller]

Got it

No problem with that. I actually prefer the idea of doing this manually because I think it would be beneficial/interesting to see exactly what's going on (the integrator libraries sort of hide this). It is also what my own supervisor suggested for the previous model (before I used an integrator library)Ok. I have never coded something like this manually. I have seen examples of CN being implemented in python though so I can follow theseIs this not what we did in the previous model? Solve for all values across all tanks at a single time before continuing to the next time step?

Lastly, if the available integrators won't do one tank at a time in sequence, why choose this approach? What is the advantage of this?

Actually, I was mistake about all this. Sorry. There is no reason why the automatic integrator can't be used if the time derivatives of the dependent variables are calculated in the proper sequence. In particular, 1. all the time derivatives for a given tank (value of z) are calculated first, and then 2. the value of $\dot{m_j}$ is calculated for that tank before moving on to the next tank.

I don't know how I didn't realize that, and I almost led you astray. Again, sorry.

Regarding the automatic integrators, they are much more preferable than ad hoc user integration schemes because (a) they make things so easy, only requiring you to provide code for calculating the time derivatives based on the solution vector, (b) they have automatic error (accuracy) control, (c) they have automatic step size control, (d) they have automatic order control, and (e) they are stable. So they are very efficient and powerful. There is no reason why you can't study the literature (e.g., the literature on the Gear integrator) to get an understanding of how this is all accomplished.

To be clearer on the above question, I'm asking -
Why did we use an integrator for the previous model rather than manually code it, and why is this approach not being used this time around. i.e. what is different between the two models that it is better to manually code CN this time?

My mistake. Stick with the automatic integrator.

 

[casualguitar]

There is no reason why the automatic integrator can't be used if the time derivatives of the dependent variables are calculated in the proper sequence. In particular, 1. all the time derivatives for a given tank (value of z) are calculated first, and then 2. the value of mj˙ is calculated for that tank before moving on to the next tank.

So $\dot{m_j}$ is the last thing to be calculated for a given tank for a given time step. Understood. However the order of calculation of time derivatives isn't clear to me yet. Does the order actually matter here? Or should it be:
1) the gas and solid phase heat balances are solved first simultaneously
2) the gas and solid deposition mole balances are solved (not simultaneously they can be solved independently)
3) $\dot{m_j}$ for the tank is solved
4) repeated for all tanks

I might be overcomplicating the below, but anyway:

So to be solved are:
- 3 gas phase mole balances
- 3 has phase heat balances
- 1 bed heat balance
- 2 solid phase heat balance (CO2 and H2O)
- 3 'molar flow out of tank' equations

The initial and boundary conditions would be (assuming the bed is initially cold and just has nitrogen in it):

ICs:
- molar holdup of nitrogen
- bed temperature
- nitrogen temperature (same at the bed temperature initially)
- mole fraction of nitrogen (equal to 1 in this case)

BCs:
- molar flow of each component into the bed
- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

So at each point in the bed we are solving for
- the mole fraction of component i (N2,H2O, CO2). We will get three y values at each point
- bed temperature
- temperature of the gas (all components assumed at the same temperature)
- total deposition (moles) of component i
- molar flow of component i

And in addition, the computational flow for solving the system of ODEs mentioned above applies to all components individually i.e. there is no dependence of one component on another? So we are solving the mass/heat balances for each component as if the other components were not present

Is this a reasonable summary?

 

[Chestermiller]

So $\dot{m_j}$ is the last thing to be calculated for a given tank for a given time step. Understood.

The j refers to the tank number, not the component number.

However the order of calculation of time derivatives isn't clear to me yet. Does the order actually matter here? Or should it be:
1) the gas and solid phase heat balances are solved first simultaneously
2) the gas and solid deposition mole balances are solved (not simultaneously they can be solved independently)
3) $\dot{m_j}$ for the tank is solved
4) repeated for all tanks

No. When using the automatic integrator, all dependent variables are being solved for simultaneously.

I might be overcomplicating the below, but anyway:

So to be solved are:
- 3 gas phase mole balances

No. Only 2: H2O and CO2. The nitrogen mole fraction is 1 minus the other two.

- 3 has phase heat balances

No. There is only one overall gas phase heat balance.

- 1 bed heat balance
- 2 solid phase heat balance (CO2 and H2O)

No. The solid phase heat balance is not solved at all. The heat generated in condensing and evaporation are distributed to the gas- and bed heat balances (by the heat flow equations I gave).

- 3 'molar flow out of tank' equations

No. There is only one molar flow out-of-tank equation. The j is the tank number , not the component number.

The initial and boundary conditions would be (assuming the bed is initially cold and just has nitrogen in it):

ICs:
- molar holdup of nitrogen
- bed temperature
- nitrogen temperature (same at the bed temperature initially)
- mole fraction of nitrogen (equal to 1 in this case)

BCs:
- molar flow of each component into the bed
- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

Yes.

So at each point in the bed we are solving for
- the mole fraction of component i (N2,H2O, CO2). We will get three y values at each point

No. Only H2O and CO2 mole fractions are solved for.

- bed temperature
- temperature of the gas (all components assumed at the same temperature)
- total deposition (moles) of component i
- molar flow of component i

If, by the latter, you mean the molar flow of component I out of the tank, then no. Even the total molar flow out of each tank is not an integrated time-dependent variable. It is just used to get the total molar flow into the next tank (for the gas phase heat balance in the next tank).

The variables that we are integrating with respect to time at all locations along the column (i.e., all tanks) are

The mole fractions of CO2 and H2O in the gas
The moles of CO2 and H2O deposited per unit area of bed (or per unit volume of column)
The temperature of the gas phase
The temperature of the bed

So there are only 6 coupled time derivatives being integrated per tank.

And in addition, the computational flow for solving the system of ODEs mentioned above applies to all components individually i.e. there is no dependence of one component on another? So we are solving the mass/heat balances for each component as if the other components were not present

The heat balances do not apply to all components individually.

 

[casualguitar]

No. When using the automatic integrator, all dependent variables are being solved for simultaneously.

Interesting ok I'll have to get my head around this one. Will take a look at the documentation to see what exactly is going on to solve these

No. Only 2: H2O and CO2. The nitrogen mole fraction is 1 minus the other two.

Got it

No. There is only one overall gas phase heat balance.

Understood yes I should have spotted that given the temperatures of N2,CO2 and H2O are assumed the same

No. The solid phase heat balance is not solved at all. The heat generated in condensing and evaporation are distributed to the gas- and bed heat balances (by the heat flow equations I gave).

Ah I think this is a terminology mix up. By solid phase heat balance I mean the bed heat balance. So its correct to say the solid deposition heat balance is not solved, but the solid bed (the packed bed) heat balance is i.e. this equation:

No. There is only one molar flow out-of-tank equation. The j is the tank number , not the component number.

So is it correct to say the assumption of constant composition in the gas phase applies here i.e. when we solve for molar flow out of the tank it is assumed that the flow composition will be the same as the inlet composition, just scaled for the different flowrate?

No. Only H2O and CO2 mole fractions are solved for.

Got it

If, by the latter, you mean the molar flow of component I out of the tank, then no. Even the total molar flow out of each tank is not an integrated time-dependent variable. It is just used to get the total molar flow into the next tank (for the gas phase heat balance in the next tank).

I did mean that yes. Ok understood

The variables that we are integrating with respect to time at all locations along the column (i.e., all tanks) are

The mole fractions of CO2 and H2O in the gas
The moles of CO2 and H2O deposited per unit area of bed (or per unit volume of column)
The temperature of the gas phase
The temperature of the bed

So there are only 6 coupled time derivatives being integrated per tank.

ICs:
- molar holdup of nitrogen
- bed temperature
- nitrogen temperature (same at the bed temperature initially)
- mole fraction of nitrogen (equal to 1 in this case)

BCs:
- molar flow of each component into the bed
- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

So if we are not solving any nitrogen related equation directly, I suppose the initial conditions should be adjusted to be:
- molar holdup of H2O and CO2 (both zero initially)
- bed temperature
- nitrogen/CO2/H2O temperature
- mole fractions of H20 and CO2 (both zero initially)

Is it a reasonable next step to solve this set of 6 equations, in a basic way assuming constants instead of using the correlations where possible)? Just to see how these equations themselves will be solved i.e. setting up initial/boundary conditions etc. Then I could build on it by gradually adding in the correlations/expressions

 

[Chestermiller]

Interesting ok I'll have to get my head around this one. Will take a look at the documentation to see what exactly is going on to solve these

Got it

Understood yes I should have spotted that given the temperatures of N2,CO2 and H2O are assumed the same

Ah I think this is a terminology mix up. By solid phase heat balance I mean the bed heat balance. So its correct to say the solid deposition heat balance is not solved, but the solid bed (the packed bed) heat balance is i.e. this equation:
View attachment 300157

So is it correct to say the assumption of constant composition in the gas phase applies here i.e. when we solve for molar flow out of the tank it is assumed that the flow composition will be the same as the inlet composition, just scaled for the different flowrate?

This has nothing to do with composition. It says that the total number of moles exiting the tank per unit time is equal to the total number of moles per unit time entering minus the rate of change in the number of moles as a result of the rate of temperature increase at constant pressure, and minus the molar rates of solid- and liquid deposition onto the bed.

Got it

I did mean that yes. Ok understoodSo if we are not solving any nitrogen related equation directly, I suppose the initial conditions should be adjusted to be:
- molar holdup of H2O and CO2 (both zero initially)
- bed temperature
- nitrogen/CO2/H2O temperature
- mole fractions of H20 and CO2 (both zero initially)

Is it a reasonable next step to solve this set of 6 equations, in a basic way assuming constants instead of using the correlations where possible)?

You realize that there are 6 times the number of tanks number of coupled ODEs being solved, right? This involves the solution of 6 times the number of tanks non-linear algebraic equations being solved at each time step.

I guess you can start out by assuming constant values for the heat transfer coefficients and mass transfer coefficients. The actual coding for these could be added later within the derivative determination subroutine.

 

[casualguitar]

This has nothing to do with composition. It says that the total number of moles exiting the tank per unit time is equal to the total number of moles per unit time entering minus the rate of change in the number of moles as a result of the rate of temperature increase at constant pressure, and minus the molar rates of solid- and liquid deposition onto the bed.

Agreed that this is unrelated to composition. However we mentioned earlier that we're not tracking composition changes in the gas phase so would this exiting molar flow technically be of the same composition as the inlet flow. Yes we will lose some of each component to the solid phase, however is it correct to say we assume that this does not affect the gas phase composition?

You realize that there are 6 times the number of tanks number of coupled ODEs being solved, right? This involves the solution of 6 times the number of tanks non-linear algebraic equations being solved at each time step.

So we have 6 ODEs here, and 2 ODEs in the last model, would that be 3 times the number of ODEs being solved? Or am I missing something? But yes it does seem like this could add significantly to the computation time. That said, we don't need thermo to calculate T(H,P) or the density/enthalpy derivative. I think these were quite costly so hopefully this balances out somewhat.

I guess you can start out by assuming constant values for the heat transfer coefficients and mass transfer coefficients. The actual coding for these could be added later within the derivative determination subroutine.

Agreed yes I think constant U, mass transfer coefficient and even constant Cp just to see how the code for this will look. Will start coding on this system tomorrow morning!

 

[Chestermiller]

Agreed that this is unrelated to composition. However we mentioned earlier that we're not tracking composition changes in the gas phase so would this exiting molar flow technically be of the same composition as the inlet flow. Yes we will lose some of each component to the solid phase, however is it correct to say we assume that this does not affect the gas phase composition?

This is included in the overall molar balance. No assumptions are made about the composition of the molar flux.

So we have 6 ODEs here, and 2 ODEs in the last model, would that be 3 times the number of ODEs being solved?

Sure

Agreed yes I think constant U, mass transfer coefficient and even constant Cp just to see how the code for this will look. Will start coding on this system tomorrow morning!

The equation F in BSL table 19.2-4 and Exercise 19D.2 seem to suggest that Cp should be evaluated at the existing overall molar composition as $\sum{y_iC_{P,i}}$.

I should also point out that, in BSL, the molar flux is defined in terms of the mass transfer coefficient by $$\dot{M}_i^"=k_i\left(y_i-\frac{p_i(T)}{P}\right)$$ where $k_i$ has units of moles/m^2s. Under these definitions, the Sherwood number for a porous medium (for use in conjunction with the correlation equation) would be defined as $$\frac{k_iD_p}{(1-\epsilon)cD_i\psi}$$ where, in BSL notation, $$c=\rho_{m}=\frac{P}{RT_I}$$

BSL point out that $cD_i$ is much less dependent on temperature than $D_i$.

 

[casualguitar]

This is included in the overall molar balance. No assumptions are made about the composition of the molar flux.

Sorry yes I understand now

The equation F in BSL table 19.2-4 and Exercise 19D.2 seem to suggest that Cp should be evaluated at the existing overall molar composition as ∑yiCP,i.

Ok can do, this seems easy enough to implement anyway.

I could use the tank j-1 position composition to evaluate Cp at tank j as $\sum{y_iC_{P,i}}$. But yes for now I'll leave it constant to simplify, unless there is a reason not to do this. I'd like to solve the ODEs with as little 'surrounding calculations' as possible

I should also point out that, in BSL, the molar flux is defined in terms of the mass transfer coefficient by M˙i"=ki(yi−pi(T)P) where ki has units of moles/m^2s. Under these definitions, the Sherwood number for a porous medium (for use in conjunction with the correlation equation) would be defined as kiDp(1−ϵ)cDiψ where, in BSL notation, c=ρm=PRTI

BSL point out that cDi is much less dependent on temperature than Di.

Understood. I'll switch to this approach then for the mass transfer coefficient function

So in summary for this iteration of this model:

Two mole balances (H2O and CO2):

Two solid phase balances (H2O and CO2):

One gas phase and one bed heat balance:

I am tempted to avoid using pythons thermo as much as possible here so save on computation cost and also confusion regarding the solid phase. I think given that thermo can't 'see' the solid phase it will cause some issues down the line so it might be best here to define some other curves manually rather than having to deal with the thermo black box:
- The gas phase N2, H2O and CO2 density curves
- The ideal gas heat capacity curves for N2, H2O and CO2

Is this reasonable?

The only place we will need nitrogen data is in the gas phase heat balance is this correct?

Also we can leave out the CO2 condensation curve completely as we're not in a pressure range that would allow this to occur

As constant in this first iteration of the model (just solving the ODEs really for now) could be the ideal gas heat capacity values, the mass transfer coefficient, component densities, and the heat transfer coefficients

Lastly the initial and boundary conditions are:

ICs:
- molar holdup of H2O and CO2 (both zero initially)
- bed temperature
- gas temperature (= bed temperature)
- mole fractions of H20 and CO2 (both zero initially)

BCs:
- molar flow of each component into the bed
- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

Does the above look reasonable to you?

 

[Chestermiller]

Sorry yes I understand now

Ok can do, this seems easy enough to implement anyway.

I could use the tank j-1 position composition to evaluate Cp at tank j as $\sum{y_iC_{P,i}}$.

No. These are at the j position. In the derivative subroutine coding for the j'th tank, the solution vector has values for the y's in the j'th tank.
No. Let the automatic integrator do it all for you.

Understood. I'll switch to this approach then for the mass transfer coefficient function

So in summary for this iteration of this model:

Two mole balances (H2O and CO2):
View attachment 300204
Two solid phase balances (H2O and CO2):
View attachment 300207
One gas phase and one bed heat balance:
View attachment 300209
View attachment 300208

- The gas phase N2, H2O and CO2 density curves
- The ideal gas heat capacity curves for N2, H2O and CO2

You're not going to have N2 condense, are you? Why do you need the gas phase densities of the N2, H20, and CO2.

Is this reasonable?

The only place we will need nitrogen data is in the gas phase heat balance is this correct?

Why do we need it in the gas phase heat balance. The molar density of the gas phase is P/RT, where P is the total pressure.

Also we can leave out the CO2 condensation curve completely as we're not in a pressure range that would allow this to occur

Correct.

As constant in this first iteration of the model (just solving the ODEs really for now) could be the ideal gas heat capacity values, the mass transfer coefficient, component densities, and the heat transfer coefficients

Lastly the initial and boundary conditions are:

ICs:
- molar holdup of H2O and CO2 (both zero initially)
- bed temperature
- gas temperature (= bed temperature)
- mole fractions of H20 and CO2 (both zero initially)

BCs:
- molar flow of each component into the bed

Just total molar flow and mole fractions. Tuinier uses mole fractions.

- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

Does the above look reasonable to you?

Yes.

 

[casualguitar]

No. These are at the j position. In the derivative subroutine coding for the j'th tank, the solution vector has values for the y's in the j'th tank.
No. Let the automatic integrator do it all for you.

Ok I don't fully understand yet how we can use j position composition values to calculate j position Cp values. I guess this is possible with implicit integrators however I don't have a picture of how this works in my head yet. Will be reading the documentation soon

You're not going to have N2 condense, are you? Why do you need the gas phase densities of the N2, H20, and CO2.

No N2 condensation, however if we're calculating the mass holdup in the heat balance then I thought we would calculate this with density correlations for each of N2,CO2 and H2O however as you have said we can use P/RT here

Just total molar flow and mole fractions. Tuinier uses mole fractions.

Got it, total molar flow and mole fractions, as these will give us the individual component flows of CO2 and H2O for the mass balances

Yes.

Ok great

 

[casualguitar]

Hi Chet, just letting you know I was sidetracked by some other work. Will be back on the ODE code tomorrow morning

 

[casualguitar]

Hi Chet, just letting you know I was sidetracked by some other work. Will be back on the ODE code tomorrow morning

Hi Chet, just updating - working on the code now. I didn't really understand what I was doing first time around with regards to using the ODE solver to solve position dependent ODEs, so I'm taking my time on it this time around i.e. I understand how to use the integrator to solve ODEs where there is no spatial discretisation, but adding in spatial discretisation from the coding point of view is difficult

 

[Chestermiller]

Hi Chet, just updating - working on the code now. I didn't really understand what I was doing first time around with regards to using the ODE solver to solve position dependent ODEs, so I'm taking my time on it this time around i.e. I understand how to use the integrator to solve ODEs where there is no spatial discretisation, but adding in spatial discretisation from the coding point of view is difficult

Not really. Discretizing with respect to the position variable z reduces the equations from a set of PDEs to a set of ODEs. This is the Method of Lines.

 

[Chestermiller]

The solution vector consists of a single column vector containing the values of all the time-integrated variables in all the tanks. When you use an automatic integrator, you furnish the integrator with a subroutine which has the solution vector in its calling sequence and which has the coding for mapping the solution vector into a column vector of the time-derivative of the solution vector.

In such a subroutine, I would start out by decomposing the solution vector into the temperatures, mole fractions, and amounts of deposits in the tanks using meaningful tank-indexed parameters like T's, y's, and M's. Then, I would calculate the time derivatives of these using our balanced equations, in terms of dT/dt's, dy/dt's, and dM/dt's. Then I would remap (recompose) these into a single time derivative column vector.

I hope this makes sense.

 

[casualguitar]

The solution vector consists of a single column vector containing the values of all the time-integrated variables in all the tanks. When you use an automatic integrator, you furnish the integrator with a subroutine which has the solution vector in its calling sequence and which has the coding for mapping the solution vector into a column vector of the time-derivative of the solution vector.

In such a subroutine, I would start out by decomposing the solution vector into the temperatures, mole fractions, and amounts of deposits in the tanks using meaningful tank-indexed parameters like T's, y's, and M's. Then, I would calculate the time derivatives of these using our balanced equations, in terms of dT/dt's, dy/dt's, and dM/dt's. Then I would remap (recompose) these into a single time derivative column vector.

Yep this makes complete sense. It is setting up the various arrays in such a way that it is possible/easy to remap them that it difficult (the mass balances are dependent on the number of species but the heat balances are not so it seems to make setting up this subroutine a bit awkward). I will post my pseudocode for this today

 

[Chestermiller]

Please, first show me what your tentative layout of the solution vector looks like.

 

[casualguitar]

Just some questions on the mass flow out of a tank equation:

This term has a time derivative on the RHS. Is it correct to say that:
1) The time derivative term in this equation comes from solving the gas phase heat balance for $\frac{\partial T_g}{dt}$ and subbing it in here?
2) We will not be including this equation in the integration itself, but just using it to link the flows between tanks

 

[Chestermiller]

Just some questions on the mass flow out of a tank equation:
View attachment 300643
This term has a time derivative on the RHS. Is it correct to say that:
1) The time derivative term in this equation comes from solving the gas phase heat balance for $\frac{\partial T_g}{dt}$ and subbing it in here?

Yes, the heat balance for tank j.

2) We will not be including this equation in the integration itself, but just using it to link the flows between tanks

Yes. It is the last thing you calculate before moving on to calculate the derivatives for the next tank.

 

[casualguitar]

Yes, the heat balance for tank j.

Yes. It is the last thing you calculate before moving on to calculate the derivatives for the next tank.

Just commenting to say I'm still working on the code. Should have pseudocode by tomorrow

 

[casualguitar]

Just commenting to say I'm still working on the code. Should have pseudocode by tomorrow

Hi Chet, yet another update from me that I am still working on the code (other things came up like experimental work, moving house etc also)

 

[casualguitar]

Hi Chet, yet another update from me that I am still working on the code (other things came up like experimental work, moving house etc also)

Just to fill you in slightly on where I'm at - I am trying to set up two functions that set up the ODEs for:
1) the initial/boundary conditions
2) the rest of the system

Here is the function for 'the rest of the system'. Note I have left some non constants as constants just because this is really pseudocode i.e. getting the structure right

I should do something similar for the initial/boundary conditions, however I'm a bit stuck as for how to split up the boundary and initial conditions. Working on it though. For reference here is the current 'initial ODE system' code which sets up the ODEs at t=0 which may not make much sense currently:

Working on it

 

[casualguitar]

Yes, the heat balance for tank j.

Yes. It is the last thing you calculate before moving on to calculate the derivatives for the next tank.

Hey Chet, hope alls well with you.

My apologies, I'm really struggling to set up these initial/boundary conditions. I have found effectively no examples online of solve_ivp being used in this way.

Is it reasonable to implement a simple explicit Euler instead here? I might have to play with the dt depending on the systems stiffness but it would give a first solution. Maybe not too accurate but we could go from there

Are there any big reasons to stick with the automatic integrator?

 

[casualguitar]

Hey Chet, hope alls well with you.

My apologies, I'm really struggling to set up these initial/boundary conditions. I have found effectively no examples online of solve_ivp being used in this way.

Is it reasonable to implement a simple explicit Euler instead here? I might have to play with the dt depending on the systems stiffness but it would give a first solution. Maybe not too accurate but we could go from there

Are there any big reasons to stick with the automatic integrator?

Just posting the updates we had over private message -
- boundary condition issues solved
- working on the property/dimensionless number functions

Question:
Just doing the $h_{fs}$ function currently which takes $Pr$, $Re$ and $k_g$ as inputs.

For the $k_g$ value, is it reasonable to use a mole fraction averaged $k_g$ value here? I.e. take the feed mole fractions of CO2, H2O and N2, calculate $k_g$ of each at the given temperature and then return a mole fraction weighted $k_g$ value?

Edit: This would mean I should write correlation functions for N2 also (cp, mu, rho, etc). I have avoided that up until now because N2 is not present in the ODEs

Edit2: Is it also correct to say that $h_{fs}$ is completely independent of the solid properties?

 

[Chestermiller]

Just posting the updates we had over private message -
- boundary condition issues solved
- working on the property/dimensionless number functions

Question:
Just doing the $h_{fs}$ function currently which takes $Pr$, $Re$ and $k_g$ as inputs.
View attachment 301632

Where is the Dp?

For the $k_g$ value, is it reasonable to use a mole fraction averaged $k_g$ value here? I.e. take the feed mole fractions of CO2, H2O and N2, calculate $k_g$ of each at the given temperature and then return a mole fraction weighted $k_g$ value?

This is only going to be approximate. In any event, BSL gives mixing rules for k.

Edit: This would mean I should write correlation functions for N2 also (cp, mu, rho, etc). I have avoided that up until now because N2 is not present in the ODEs

This doesn't seem like a big deal.

Edit2: Is it also correct to say that $h_{fs}$ is completely independent of the solid properties?

Of course.

 

[casualguitar]

Where is the Dp?

Typo (this was included in the previous model)

This equation returns $h_{fs}$ values in the $200-1000W/m2K$ range for typical Reynolds numbers (up to $10^4$)

This doesn't seem like a big deal.

Yes its not

Of course.

Nice. Except for the particle diameter I suppose if that is considered to be a solid property

Anyway I'm almost there with these functions. I think I'll post plots of them all with typical dependent variable ranges just to confirm they're all working as expected before moving on.

For reference, the plots will roughly include:

 

[casualguitar]

For the mass transfer coefficient, I'm confused regarding the reason we need to calculate the Sherwood number. Heres the flow currently:

So we calculate the Re and Sc numbers. Then the mass transfer coefficient $k_i$ seems to be a function of just these two numbers, so why the need to calculate the Sherwood number? And is Sh actually equal to $k_f$?

 

[casualguitar]

So I worked back through the mass transfer coefficient correlation derivation (my post above was a load of nonsense in hindsight, apologies). I almost have it but have uncertainty about which Sh number correlation to use. Heres the derivation (I just read back over the heat transfer coefficient derivation you did as its analogous to the mass transfer coefficient):

1) Define Sc and Re
$Re = \frac{6G_0}{a\mu\Psi}$
$Sc = \frac{\mu}{\rho D}$

2) Define the sherwood number
$Sh = \frac{k_id_p}{\rho_mD_{ab}}$

I took this one from BSL. I know you defined another Sh number earlier which was:
$Sh_{loc,i}=\frac{k_iD_p}{(1-\epsilon_g)D_i\psi}$

Its easy to interchange between the two but I am not sure of the reason to use one over the other

Anyway

3) Defining the CC factor $j_D$ as:
$j_D = ShRe^{-1}Sc^{-1/3}$

4) And the same specifically for packed beds:
$j_D = 2.19Re^{-2/3} + 0.78Re^{-0.381}$

5) Letting 3 equal to 4 and solving for k_i:
$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{a,b}\frac{\rho}{d_p}$

Is this correct? I can easily sub in your Sh number instead of the BSL one, but what is the reason you did not use the BSL one?

 

[Chestermiller]

So I worked back through the mass transfer coefficient correlation derivation (my post above was a load of nonsense in hindsight, apologies). I almost have it but have uncertainty about which Sh number correlation to use. Heres the derivation (I just read back over the heat transfer coefficient derivation you did as its analogous to the mass transfer coefficient):

1) Define Sc and Re
$Re = \frac{6G_0}{a\mu\Psi}$
$Sc = \frac{\mu}{\rho D}$

2) Define the sherwood number
$Sh = \frac{k_id_p}{\rho_mD_{ab}}$

I took this one from BSL. I know you defined another Sh number earlier which was:
$Sh_{loc,i}=\frac{k_iD_p}{(1-\epsilon_g)D_i\psi}$

Its easy to interchange between the two but I am not sure of the reason to use one over the other

Anyway

3) Defining the CC factor $j_D$ as:
$j_D = ShRe^{-1}Sc^{-1/3}$

4) And the same specifically for packed beds:
$j_D = 2.19Re^{-2/3} + 0.78Re^{-0.381}$

5) Letting 3 equal to 4 and solving for k_i:
$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{a,b}\frac{\rho}{d_p}$

Is this correct? I can easily sub in your Sh number instead of the BSL one, but what is the reason you did not use the BSL one?

The approach I'm recommending is based on Reynolds analogy, and I think it is better. I don't think that BSL considered this.

I believe your eon 5 is correct if dp is calculated by the definition in BSL.

 

[casualguitar]

The approach I'm recommending is based on Reynolds analogy, and I think it is better. I don't think that BSL considered this.

I believe your eon 5 is correct if dp is calculated by the definition in BSL.

Hmm I'm taking the characteristic length from the Sherwood number $l_0$ to be $d_p$, the particle diameter. Why would dp be calculated using the BSL definition? Or have I misunderstood. The units for $k_i$ I have are $mol/m2.s$ not $m/s$ so I guess I am mistaken somewhere here

Also I'm effectively finished the function write ups and plots. I have the mass transfer coefficient one to confirm correct, then the mass deposition one is built on this so I have that also. Besides that I have two small questions regarding $U_b$ and $U_g$

So $U_b$ will be a constant times the thermal conductivity divided by the particle diameter. This constant is $\beta$ I presume, which is equal to 10 for spheres, meaning that we would get $U_b = \frac{\beta k_p}{d_p}$?

For $U_g$ we can evaluate this at the bulk gas temperature. I have taken the exact same correlation as we had in the previous model. However you mentioned we would have a correction factor involving viscosity at the interface this time? Why would we have this?

 

[Chestermiller]

Hmm I'm taking the characteristic length from the Sherwood number $l_0$ to be $d_p$, the particle diameter. Why would dp be calculated using the BSL definition? Or have I misunderstood. The units for $k_i$ I have are $mol/m2.s$ not $m/s$ so I guess I am mistaken somewhere here

I had this worked out a few weeks ago, but don't quite remember now. You need to look at the table in BSL that has various versions of this in there. If I remember correctly, it is almost certainly the $mol/m2.s$ that we should be using. You need to play with the different versions until you arrive at the one that makes sense to you.

Also I'm effectively finished the function write ups and plots. I have the mass transfer coefficient one to confirm correct, then the mass deposition one is built on this so I have that also. Besides that I have two small questions regarding $U_b$ and $U_g$

So $U_b$ will be a constant times the thermal conductivity divided by the particle diameter. This constant is $\beta$ I presume, which is equal to 10 for spheres, meaning that we would get $U_b = \frac{\beta k_p}{d_p}$?

Yes, I think so.

For $U_g$ we can evaluate this at the bulk gas temperature. I have taken the exact same correlation as we had in the previous model. However you mentioned we would have a correction factor involving viscosity at the interface this time? Why would we have this?

See BSL section on heat transfer for turbulent flow in a pipe.

 

[casualguitar]

The approach I'm recommending is based on Reynolds analogy, and I think it is better. I don't think that BSL considered this.

I believe your eon 5 is correct if dp is calculated by the definition in BSL.

Ok got it I think. So using BSLs Sherwood number is ok, however the Reynolds analogy approach you used is better, meaning that $k_i$ would go from this with the BSL Sherwood number of $Sh_{loc,i} = \frac{k_id_p}{\rho_mD_{ab}}$:
$$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{a,b}\frac{\rho}{d_p}$$

To this, with your Sherwood number of $Sh_{loc,i}=\frac{k_id_p}{(1-\epsilon_g)D_i\psi}$:
$$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}(1-\epsilon_g)D_i\frac{\psi}{d_p}$$

How would I assess which Sh correlation is better? I could plot one against the other for a range of $k_i$ values and see if they are almost equivalent. However if one returns appreciably higher values than the other I am not sure how to assess which is the better of the two

 

[casualguitar]

You need to play with the different versions until you arrive at the one that makes sense to you.

Yes any version I have tried has produced $mol/m^2.s$ so I'll go with this for now unless I see an inconsistency

Yes, I think so.

See BSL section on heat transfer for turbulent flow in a pipe.

Great, will do that this morning

Edit: Found those correlations. They give the laminar (Re<2100) and highly turbulent flow equations (Re>20000). The transition flow region is only available from a graph (no equation provided I don't think). The Re number for this system seems to be in the region of 20000 or so anyway, so for simplicity I will take the turbulent flow equation rather than extracting the relevant equation from the graph. That equation for forced convection and turbulent flow in tubes (and L/D > 10) is:
$$Nu_{ln} = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}$$
where $\mu_b$ is the bulk viscosity and $\mu_0$ is the surface viscosity which are I guess evaluated at the solid and fluid temperatures respectively?

So, this would mean the new $U_g$ heat transfer coefficient would be:
$$U_g = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}\frac{k_g}{d_p}$$

For reference, the previous model HTC was:
$$U_g = (2.19Re^{1/3} + 0.78Re^{0.66})Pr^{1/3}\frac{k_g}{d_p}$$

 

[casualguitar]

Lastly, regarding the units of ki, any equation with ki in it shows that the unit of ki is $mol/m^2.s$. However, the molar desublimation rate formula $\dot{M}_i^"=k_i\left(\frac{Py_i-p_i(T_I)}{RT_I}\right)\tag{1}$ suggests that the units are $m/s$. If this is correct, is there an equivalent molar desublimation rate equation that would use units of mol/m2.s for ki?

For reference, my units are:
$k_i$ = $mol/m^2.s$
$P$ = $Pa$
$y_i$ = $mol/mol$
$R$ = $J/mol.K$
$T$ = $K$

 

[Chestermiller]

Yes any version I have tried has produced $mol/m^2.s$ so I'll go with this for now unless I see an inconsistencyGreat, will do that this morning

Edit: Found those correlations. They give the laminar (Re<2100) and highly turbulent flow equations (Re>20000). The transition flow region is only available from a graph (no equation provided I don't think). The Re number for this system seems to be in the region of 20000 or so anyway, so for simplicity I will take the turbulent flow equation rather than extracting the relevant equation from the graph. That equation for forced convection and turbulent flow in tubes (and L/D > 10) is:
$$Nu_{ln} = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}$$
where $\mu_b$ is the bulk viscosity and $\mu_0$ is the surface viscosity which are I guess evaluated at the solid and fluid temperatures respectively?

So, this would mean the new $U_g$ heat transfer coefficient would be:
$$U_g = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}\frac{k_g}{d_p}$$

For reference, the previous model HTC was:
$$U_g = (2.19Re^{1/3} + 0.78Re^{0.66})Pr^{1/3}\frac{k_g}{d_p}$$

No. No. The correlation you chose is for flow in a pipe, not a packed bed. You should continue to use the packed bed correlation, but just apply the wall viscosity correction.

 

[casualguitar]

No. No. The correlation you chose is for flow in a pipe, not a packed bed. You should continue to use the packed bed correlation, but just apply the wall viscosity correction.

Ah ok so it would be $U_{g,NEW} = U_{g,OLD}*\frac{\mu_b}{\mu_0}^{0.14}$?