- #351
- 23,583
- 5,819
No. The k correlation.casualguitar said:
Modelling of two phase flow in packed bed (continued)
- Thread starter casualguitar
- Start date
In summary: I don't know actually, but I think you will be right about the CO2 depositing temporarily on the bed. What I thought would happen (assuming a bed colder than the freezing point of CO2) was that the ambient CO2 enriched stream would enter the cold bed and immediately the CO2 at the 'front' of the stream would freeze. The pure air would carry on through the bed. Then the newly entering stream - which is at ambient temperature - would vaporise the frozen CO2, and the vaporised CO2 plus the CO2 'behind' it in the stream would now be frozen/deposited slightly further downstream. This process repeats until you
- #352
casualguitar
- 503
- 26
Uncertain about the units for ##k_i## and ##D_{ab}## (mass diffusion coefficient) -Chestermiller said:
So the correlation I've currently got for ##k_i## is:
$$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{ab}\rho_m/d_p$$
The the units of ##D_{ab}## are ##m^2/s## from the correlation above. BSL provides these ##D_{ab}## values in ##m^2/s## also. The units of ##k_i## are therefore ##mol/m^2.s## then. There is probably some unit issue here somewhere because the molar deposition rate is also mol/m2.s. Can the units of ##k_i## be the same as the units of ##M_i''##?
The Schmidt number I calculated seems to be ok also when compared to BSL data. The plot produced for a range of Reynolds numbers looks like this:
For references the current constant ##k_{CO2}## value I'm using is 8*10^-4, so these seem high. Anyway I'll implement the non-constant ##k_j## functionality into the current script and let's see what happens
Last edited:
- #353
- 23,583
- 5,819
You keep flip-flopping between k having units of m/s and having units of moles/m^2.sec. If you are using m/s, leave out the ##\rho_m\ (=\frac{P}{RT_I})## in the above equation. Otherwise, keep it. I also think there should be a factor of ##(1-\epsilon)## in the above equation. Your equation for molar flux seems to use k is in m/s. Is that your understanding?casualguitar said:
You need to get the units issue resolved.casualguitar said:
Last edited:
- #354
casualguitar
- 503
- 26
That is my understanding yes. I had some issues getting the non constant ##k_i## model to converge however it does converge now. The output below is for n=5. Adding in non constant ##k_i## seems to increase the runtime of the model by quite a bit for some reason. So I'll run n=30 in a bit (currently on the way home) and see how long it takes. Anyway here's the n=5 output:Chestermiller said:
I don't like how the MCO2 plot looks (the peaks should increase in size over time), so I'll look into that. But yes first I'll run n=30
- #355
casualguitar
- 503
- 26
n = 10 with non-constant ##k_i##:casualguitar said:
No such luck getting n=30 to converge. It seems to get stuck around 180K. I'm not sure what extra difficulty would be caused be n=30 that is not present in n=10 besides maybe some convergence issues. Looking into it. I'm leaving the simulation running just on the off chance it does actually converge after long times
- #356
- 23,583
- 5,819
What implicit integrator are you using? What is the structure of the Jacobian matrix, and do you take advantage of this in the matrix inversion chosen option>casualguitar said:
- #357
casualguitar
- 503
- 26
The LSODA integrator (from the solve_ivp package). I have seen mentions of the Jacobian matrix in the documentation so I'll take a look at thisChestermiller said:
- #358
casualguitar
- 503
- 26
Hi Chet, I looked into the Jacobian matrix question and if I understand the question the structure of the Jacobian matrix is just a rectangle of shape [n,6], where n is the number of spatial positions and 6 is the number of ODEs we have. Does this answer the question?casualguitar said:
Also I'm not sure if you got the notification of the private message I sent. I attached the report as mentioned, and this also shows the Jacobian and solution array structures
What does it mean to take advantage of the structure of the Jacobian matrix in the matrix inversion chosen option?
- #359
casualguitar
- 503
- 26
Hi Chet,Chestermiller said:
As mentioned, here is the model output for the new Reynolds Number formulation:
We're now getting a clear constant temperature zone around the sublimation point of CO2, similar to the Tuinier model:
The mass buildup looks odd here in that the maximum buildup amount at a position seems to be constant, and also the value (approx 100) is about double the Tuinier value. Looking into this
- #360
- 23,583
- 5,819
This looks like a major improvement. Is the only difference the equation used to calculate the Re? It doesn't seem possible.casualguitar said:
- #361
casualguitar
- 503
- 26
Yep you're right its not possible. I was mistakenly using the inlet molar flow to calculate the non-boundary position Reynolds Numbers. In switching to your new Re formulation I noticed that mistakeChestermiller said:
The CO2 mass buildup trend is correct in that the plug of CO2 increases in 'width' over time. Is that actually an issue that it seems to stay at a constant 100kg/m3?
In checking the area values I've got one point of confusion. What is the difference between ##A_s## and ##a_s##? ##A_s## seems to be the particle surface area per unit volume: $$A_s = \frac{6}{d_p}(1-\epsilon)$$
and ##a_s## is the particle surface area per unit superficial volume of column. What is the difference between this and ##A_s##? ##a_s## might be $$a_s = \frac{4\pi r^2}{A_c\Delta z}(1-epsilon)$$?
In regards to where each are used, it seems that ##A_s## will be used everywhere here, so we don't seem to have a need for ##a_s##?
- #362
- 23,583
- 5,819
No. See their Fig. 3.casualguitar said:
That is the equation for ##a_s##, the particle surface per unit volume of column. ##A_s## is the particle surface per tank. $$A_s=A_c\Delta z a_s=\frac{6}{d_p}(1-\epsilon)A_c\Delta z$$casualguitar said:
Correct.casualguitar said:
- #363
casualguitar
- 503
- 26
Ah whoops yes I agree with the above, and I am using the correct ##A_s## value. Typo by me. Ok then its possibly time to add in the last few small bits (non constant heat capacity, non constant viscosity, etc)? I have the functions written for all of those. I don't think it will change the output much though. A reasonable next (final?) step?Chestermiller said:
GreatChestermiller said:
EDIT: Oh and I'll make that change you mentioned about including the mass flow rate derivative as an integrated variable
So now that the model is effectively ready to be used (you might disagree with that), I think it would be useful to run a number of simulations to show how some performance parameters vary with initial and boundary conditions (ICs/BCs), such as separation efficiency or CO2 captured per unit of refrigeration. Do you think it is worthwhile to do this kind of 'factorial analysis'?
Last edited:
- #364
- 23,583
- 5,819
You need to again confirm that the overall CO2 mass balance is satisfied. I'm also wondering why we get a peak of 100, and they get a peak of 60. Try 15 tanks to see whether the added axial dispersion spreads the deposited CO2 out over a broader region.casualguitar said:
As far as applying the model, I leave it up to you to decide cases to consider, although your thesis advisor should have input to this.
- #365
casualguitar
- 503
- 26
Seems to fail at around 330K. There isn't any phase change happening around there so I'm not sure why that happens. Looking into itChestermiller said:
- #366
- 23,583
- 5,819
15 tanks should run more easily than 30 tanks. Sounds like a variable dimensioning/storage issue.
- #367
casualguitar
- 503
- 26
Hi Chet! I've returned to the CO2 model and was hoping to discuss it with someone. You're the person that I've had the most discussion with on this so I was hoping I could continue this for a short while if thats ok with you! The simulation has progressed since our last discussion but there are some parts that I am unsure about. I just have some questions I'd like to discuss with someone. If this is ok with you, I can bring you up to speed on thisChestermiller said:
- #368
- 23,583
- 5,819
I'll do my best to answer your questions, but my memory of this work is fading.casualguitar said:
- #369
casualguitar
- 503
- 26
My apologies for the information dump below - these are the equations being solved and the initial/boundary values. Along with some comments at the end
And here is the model/experimental data we were tuning to at the time: https://www.sciencedirect.com/science/article/abs/pii/S0009250909000852
Here are our model equations:
The gas phase mole balance
\begin{equation}
m_j\frac{dy_i}{dt} = \dot{m}_{j-1}(y_{j-1} - y_j) - M_{i,j}''A_s + y_{i,j}\sum\limits_{i=1}^{n_c} M_{j,z}''A_s
\end{equation}
The gas phase heat balance:
\begin{equation}
m_j C_{p,j}\frac{dT_g}{dt} = \dot{m}_{j-1}C_{p,j-1}(T_{j-1} - T_j) - q_{g,I,j}A_s
\end{equation}
The bed heat balance:
\begin{equation}
M_sC_{p,s,j}\frac{dT_b}{dt} = q_{I,b,j}A_s
\end{equation}
Solid phase mass balance:
\begin{equation}
\frac{dM_i}{dt} = M_i''A_s
\end{equation}
Mass flow out of a tank:
\begin{equation}
\dot{m}_{j} = \dot{m}_{j-1} + \frac{\rho_m}{T_g}A_C\Delta z\frac{dT}{dt} - \sum\limits_{i=1}^{n_c} M_{i,j}''A_s
\end{equation}
Here are our equations for ##M_{i,j}''##, ##q_{g,I}## and ##q_{I,b}##:
\begin{equation}
M_i'' = \frac{k_i(Py_i - p_{i,T_I})}{RT}
\end{equation}
\begin{equation}
q_{g,I} = -\frac{U_g q^*}{U_g+U_b} + U^*(T_g - T_b)
\end{equation}
\begin{equation}
q_{I,b} = \frac{U_b q^*}{U_g+U_b} + U^*(T_g - T_b)
\end{equation}
We also have correlations from BSL for the mass transfer coefficient ##k_i##, the fluid solid heat transfer coefficient ##h_{f,s}## and the sublimation pressure of CO2 ##p_{sub,co2}##:
\begin{equation}
h_{fs} = (2.19Re^{1/3} + 0.78Re^{0.619})Pr^{1/3}(\frac{k_g}{d_p})(\frac{\mu_{b,T_I}}{\mu_{0,T_I}})^{0.14}(1-\epsilon)
\end{equation}
\begin{equation}
k_{i} = (2.19Re^{1/3} + 0.78Re^{0.619})\frac{Sc^{1/3}}{d_p}D_{ab}(1-\epsilon_g)
\end{equation}
\begin{equation}
ln(\frac{P_{sub}}{P_t}) = \frac{T_t}{T}[a_1(1-\frac{T}{T_t)}+a_2(1-\frac{T}{T_t})^{1.9}+a_3(1-\frac{T}{T_t})^{2.9}]
\end{equation}
I'm not sure why the equation numbers are so high, but anyway -
Right now since the output I'm getting is not as expected, I have set the mass and heat transfer coefficients to be constants. The only other big change is that we are no longer including ##H_2O## in this model, just a stream of Nitrogen and ##CO_2##.
Here are the constants, initial and boundary values as they are currently:
Constants:
U_b = 100
U_g = 50
cp_CO2 = 37
ki_CO2 = 5 * 10 ** -4 # mol/m2.s (I'm actually still not fully sure about this unit)
Initial values:
initial_co2_mole_fraction = 0.00
initial_co2_deposit = 0.0
initial_gas_temperature = 123.15
initial_bed_temperature = 123.15
Boundary Values:
molar_flow_in = 0.002
y_CO2_inlet = 0.2
T_inlet = 300
And here is the model/experimental data we were tuning to at the time: https://www.sciencedirect.com/science/article/abs/pii/S0009250909000852
Here are our model equations:
The gas phase mole balance
\begin{equation}
m_j\frac{dy_i}{dt} = \dot{m}_{j-1}(y_{j-1} - y_j) - M_{i,j}''A_s + y_{i,j}\sum\limits_{i=1}^{n_c} M_{j,z}''A_s
\end{equation}
The gas phase heat balance:
\begin{equation}
m_j C_{p,j}\frac{dT_g}{dt} = \dot{m}_{j-1}C_{p,j-1}(T_{j-1} - T_j) - q_{g,I,j}A_s
\end{equation}
The bed heat balance:
\begin{equation}
M_sC_{p,s,j}\frac{dT_b}{dt} = q_{I,b,j}A_s
\end{equation}
Solid phase mass balance:
\begin{equation}
\frac{dM_i}{dt} = M_i''A_s
\end{equation}
Mass flow out of a tank:
\begin{equation}
\dot{m}_{j} = \dot{m}_{j-1} + \frac{\rho_m}{T_g}A_C\Delta z\frac{dT}{dt} - \sum\limits_{i=1}^{n_c} M_{i,j}''A_s
\end{equation}
Here are our equations for ##M_{i,j}''##, ##q_{g,I}## and ##q_{I,b}##:
\begin{equation}
M_i'' = \frac{k_i(Py_i - p_{i,T_I})}{RT}
\end{equation}
\begin{equation}
q_{g,I} = -\frac{U_g q^*}{U_g+U_b} + U^*(T_g - T_b)
\end{equation}
\begin{equation}
q_{I,b} = \frac{U_b q^*}{U_g+U_b} + U^*(T_g - T_b)
\end{equation}
We also have correlations from BSL for the mass transfer coefficient ##k_i##, the fluid solid heat transfer coefficient ##h_{f,s}## and the sublimation pressure of CO2 ##p_{sub,co2}##:
\begin{equation}
h_{fs} = (2.19Re^{1/3} + 0.78Re^{0.619})Pr^{1/3}(\frac{k_g}{d_p})(\frac{\mu_{b,T_I}}{\mu_{0,T_I}})^{0.14}(1-\epsilon)
\end{equation}
\begin{equation}
k_{i} = (2.19Re^{1/3} + 0.78Re^{0.619})\frac{Sc^{1/3}}{d_p}D_{ab}(1-\epsilon_g)
\end{equation}
\begin{equation}
ln(\frac{P_{sub}}{P_t}) = \frac{T_t}{T}[a_1(1-\frac{T}{T_t)}+a_2(1-\frac{T}{T_t})^{1.9}+a_3(1-\frac{T}{T_t})^{2.9}]
\end{equation}
I'm not sure why the equation numbers are so high, but anyway -
Right now since the output I'm getting is not as expected, I have set the mass and heat transfer coefficients to be constants. The only other big change is that we are no longer including ##H_2O## in this model, just a stream of Nitrogen and ##CO_2##.
Here are the constants, initial and boundary values as they are currently:
Constants:
U_b = 100
U_g = 50
cp_CO2 = 37
ki_CO2 = 5 * 10 ** -4 # mol/m2.s (I'm actually still not fully sure about this unit)
Initial values:
initial_co2_mole_fraction = 0.00
initial_co2_deposit = 0.0
initial_gas_temperature = 123.15
initial_bed_temperature = 123.15
Boundary Values:
molar_flow_in = 0.002
y_CO2_inlet = 0.2
T_inlet = 300
Attachments
-
co2_unbounded.png -
position_versus_gas_temperature.png -
position_vs_bed_temperature.png -
co2_deposition_vs_position_kg.png -
Screenshot 2023-05-07 at 19.59.13.png -
Screenshot 2023-05-07 at 19.58.42.png -
Screenshot 2023-05-07 at 19.58.25.png -
Screenshot 2023-05-07 at 19.55.56.png -
Screenshot 2023-05-07 at 19.55.05.png -
Screenshot 2023-05-07 at 19.52.52.png
- #370
casualguitar
- 503
- 26
The output looks like this -
The output looks like this, for n = 200:
I wanted to incude this last plot showing every position (all 200) and how they behave over time. Clearly the CO2 mole fraction output isnt right. The other plots dont actually look too bad though.
In regards to the position vs temperature plots higher up, there doesnt seem to be any constant temperature zone which is present in Tuinier et al.
I apologise for the information dump but yes I would just like to open up dialogue here again as I found it hugely beneficial last time to have someone to have a back and forth with.
Is the above information sufficient or should I provide further info on this?
EDIT: One point I forgot to mention - in the gas/bed temperature vs position plots, I have printed time values. You can see that the temperature profile acually stops changing after a while and this is before the entirety of the bed has reached the inlet gas temperature
The output looks like this, for n = 200:
I wanted to incude this last plot showing every position (all 200) and how they behave over time. Clearly the CO2 mole fraction output isnt right. The other plots dont actually look too bad though.
In regards to the position vs temperature plots higher up, there doesnt seem to be any constant temperature zone which is present in Tuinier et al.
I apologise for the information dump but yes I would just like to open up dialogue here again as I found it hugely beneficial last time to have someone to have a back and forth with.
Is the above information sufficient or should I provide further info on this?
EDIT: One point I forgot to mention - in the gas/bed temperature vs position plots, I have printed time values. You can see that the temperature profile acually stops changing after a while and this is before the entirety of the bed has reached the inlet gas temperature
Last edited:
- #371
- 23,583
- 5,819
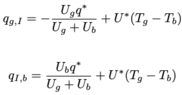
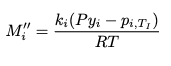
What do the results look like if you run the model with the mass transfer coefficient set to zero?casualguitar said:
- #372
casualguitar
- 503
- 26
Hi Chet, setting ki_CO2 = 0 and letting n=200 results in these plots:Chestermiller said:
The co2 mole fraction rises to 0.2 which is the inlet mole fraction, so this looks ok. There is no CO2 buildup on the bed as expected. The temperature profiles also generally look ok although there is no constant temeprature zone.
For reference, the h_desublimation_CO2 is set to 26,000 J/mol currently. Just now I tried setting it to 0 and 200,000, neither of which changed the temperature profiles appreciably
- #373
- 23,583
- 5,819
Why does the CO2 mole fraction rise so rapidly? What is the gas residence time in the bed?casualguitar said:
I feel that the problem is related to the CO2 mass transfer, particularly when the conditions are such that there is no longer CO2 remaining deposited on the bed.
- #374
casualguitar
- 503
- 26
I think due to the high flow. The inlet total molar flow for that plot was 0.002mol/s.Chestermiller said:
Here is a flow 10 times smaller. ##\dot{m_{in}}## = 0.0002mol/s
Hmm to calculate gas residence time in the bed, could we do something like:
\begin{equation}
t_{residence} = \frac{L_{BED}}{v_{gas}}
\end{equation}
The velocity of the gas is:
\begin{equation}
v_{gas} = \frac{\dot{m_{in}}}{\rho A}
\end{equation}
where ##\dot{m_{in}}## is in mol/s, ##\rho## is in mol/m3 and A is in ##m^2##
For ##L_{BED}## = 0.3m:
##v_{gas}## = 0.0002/(36.36*0.00096) = 0.005m/s
Which gives a ##t_{residence}## value of ##52.63s##Just note at this point I'm using the bed dimensions, bed initial temperature, inlet gas temperature and inlet gas CO2 mole fraction from Tuinier et al. The inlet flow, mass transfer coefficient, and heat transfer coefficients are currently not the same. I can switch to the tuinier inlet mass flux now of 0.24kg/m2.s if the above is reasonable?
- #375
- 23,583
- 5,819
There's something wrong with how the release of the CO2 from the bed is handled. If there is a driving force for removal but there is no CO2 left on the bed, the flow of CO2 from the bed to the gas has to be zero. That means that the mass balance equation for the CO2 in the gas has to allow for this. Is it?
- #376
casualguitar
- 503
- 26
No it doesn't allow for it. Right now the value can go below zero and does. Originally I had a conditional statement in the integrator that said "if the amount of CO2 in the bed goes below zero, set it to zero". Then I moved this statement to post-processing, so now I'm just plotting the CO2 deposition values that are above zero, but the solution from the integrator does contain negative values. Are either of these approaches ok, or should we somehow allow for it directly in the mass balance equation?Chestermiller said:
Right now the plots are unaffected by this (I think) since the mass transfer coefficient is zero thoughEdit: Sorry my apologies - I previously mentioned that there was no constant temperature zone. There is a constant temperature zone when the mass transfer coefficient is a non-zero value.
For reference, here's the CO2 buildup and other output when I dont post-process it to only show values greater than zero, when the mass-transfer coefficient is non-zero:
The blue line in the CO2 buildup plot is position 0, the orange one is position 1, if we continue on this plot the other positions drop off to negative values similarly. The mole fraction of CO2 goes above the inlet molar concentration of CO2. The temperature plots also look unusual
Heres the gas temperature plot, just illustrating that the constant temperature zone is present:
As you were saying there is likely an issue with how CO2 is released from the bed. How should we allow for the CO2 deposition value only being positive in the mole balance?
As mentioned, I am just post-processing the solution at the moment to remove the negative values. I can set the value to have a minimum value of zero inside the integrator though. Although I'm not sure if this is actually different to doing what I'm doing currently
Last edited:
- #377
- 23,583
- 5,819
We must set ##\frac{dM_i}{dt}=0## if ##M_i\leq 0## and ##M_i^"<0##, which is equivalent to ##M_i\leq 0## and ##(Py_{i}-p_{i,T_I})<0##. I've been trying to figure out a simple way of doing this in coding without use of IF statements.
- #378
casualguitar
- 503
- 26
There is an equivalent vectorised option in pythons numpy library called "where". Its just a vectorised if statement package though. I could replace the existing ##\frac{dM_i}{dt}## code lines (the boundary one and the internal nodes one) with something like this:
##\frac{dM_i}{dt} = np.where((M_i <= 0)## & ##(P * y_i - p_{i,T_I} < 0), 0, M_i'' * A_s)##
Which just says if the first two conditions are true then ##\frac{dM_i}{dt} = 0##, else ##\frac{dM_i}{dt} = M_i'' * A_s##
What is the reason that an IF statement isn't suitable here?
Edit: Just a note - heres the output with the above implemented. It does limit the CO2 deposited to a minimum of zero, but the mole fraction and temperature profiles are not right
Just noting also that if the mass transfer coefficient is set to zero with the new code addition then the output looks reasonable again:
##\frac{dM_i}{dt} = np.where((M_i <= 0)## & ##(P * y_i - p_{i,T_I} < 0), 0, M_i'' * A_s)##
Which just says if the first two conditions are true then ##\frac{dM_i}{dt} = 0##, else ##\frac{dM_i}{dt} = M_i'' * A_s##
What is the reason that an IF statement isn't suitable here?
Edit: Just a note - heres the output with the above implemented. It does limit the CO2 deposited to a minimum of zero, but the mole fraction and temperature profiles are not right
Just noting also that if the mass transfer coefficient is set to zero with the new code addition then the output looks reasonable again:
Last edited:
- #379
- 23,583
- 5,819
Is ##A_s## the bed surface area (m^2) per tank and ##M_I## the moles of CO2 deposited per tank? If so, pleases try to impose the following: If ##M_i<0.1 A_s## and ##M_{i}^"\leq 0##, reset ##M_i^"## to zero. This applies to the realistic flow rates.
Last edited:
- #380
casualguitar
- 503
- 26
Yes. Here is the output when this is imposed:Chestermiller said:
Where ##A_s =A_c\Delta z a_s=\frac{6}{d_p}(1-\epsilon)A_c\Delta z = 0.0032m^2##, the molar flow is 0.002mol/s and k_i = 5 * 10 ** -4 mol/m2.s:
Is the reason for the ##0.1A_s## constraint so that we dont run into any case where ##M_i## <0? In a case where ##M_i''## is large this may occur
Just a note - this is n=200. The output is very different for lower n (n=20 or so). I can clean up the plotting to plot say 10% of the total positions if needed
Attachments
Last edited:
- #381
- 23,583
- 5,819
Yes. Do you think 0.1 is too large. Why didn't you run the calculation for a realistic molar flow rate?casualguitar said:
What are your thoughts on whether the new plots were closer to your expectations?
- #382
casualguitar
- 503
- 26
No I think 0.1 is ok. Ah I was using a molar flow rate that fit the mass transfer coefficient. These two values affect the output quite a lot so if I change the molar flow I also need to adjust the mass transfer coefficient to get reasonable looking output.Chestermiller said:
The Tuinier et al reference uses 0.27kg/m2, which is 0.0083mol/s.
The Tuinier et al reference uses g = 1x10^-6 s/m. From post #233, the relationship between their g and our ##k_i## is:
\begin{equation}
k=\frac{1000RT}{M}g
\end{equation}
which gives ##k_{CO2}## = 0.047 for g = 1x10^-6.
Output using all of their values above looks like this (note the inlet temperature is 300K and the initial bed temperature is 123K):
The constant temperature zone is at approximately the right temperature, but the temperature seems to max out at around this temperature, rather than increase to the inlet gas temperature of 300K:
The bed temperature seems to start at 0K actually, but ignoring this the rest of the temperature profile seems to be about the same as the gas temperature profile. I'll look into this 0K issue now
The heat transfer profile at the inlet position (the blue one) does not look right, and the profile is very different to the internal node profiles:
The CO2 buildup profile looks ok. We dont get the same max values as Tuinier but they dont specify the simulation conditions for their CO2 buildup plot:
Investigating this 0K and heat transfer profile issue now
EDIT: That was a typo in how I was plotting the bed temperature. The ##Q_{BI}##/##Q_{IG}## issue still stands though
Attachments
Last edited:
- #383
casualguitar
- 503
- 26
Just one addition to the above - letting ki_CO2 = 0 results in output that looks as expected. So yes as you said its definitely related to how co2 is released from the bed:
The CO2 moves through the bed quickly as there is no desublimation:
The CO2 moves through the bed quickly as there is no desublimation:
- #384
casualguitar
- 503
- 26
The issue is with MDR (as you said previously). The molar desublimation rate at the inlet position does not trend towards zero as the other positions do. I will come back to this later this evening and see if the MDR function is implemented differently at the boundary
Here's the function:
Here's the function:
- #385
casualguitar
- 503
- 26
Hi Chet,
Just noting one other thing in regards to the CO2 flow through the bed (molar flow/molar holdup).
The molar flow out of the first tank is currently calculated as:
which is the molar flow into tank 1 minus the total amount of CO2 deposited/released in that tank
Similarly, the molar flow out of the internal tanks is as follows:
It looks ok to me but I'm just confirming this is correct
EDIT: I know why the heat transfer profiles (QGI and QIB) look the way they do. The gas/bed temperature plots get stuck at around the sublimation temperature, meaning that there will always be high heat transfer between the inlet gas and the first tank. The remaining tanks are at almost the same temperature as the first tank which is why we only see high heat transfer in the first one. That doesn't solve the problem but it does explain the QGI/QIB plots
EDIT 2: Whoops!! The molar flow out of the tank is wrong! I'm going to take a look at this tomorrow when I have a clear head
Just noting one other thing in regards to the CO2 flow through the bed (molar flow/molar holdup).
The molar flow out of the first tank is currently calculated as:
which is the molar flow into tank 1 minus the total amount of CO2 deposited/released in that tank
Similarly, the molar flow out of the internal tanks is as follows:
It looks ok to me but I'm just confirming this is correct
EDIT: I know why the heat transfer profiles (QGI and QIB) look the way they do. The gas/bed temperature plots get stuck at around the sublimation temperature, meaning that there will always be high heat transfer between the inlet gas and the first tank. The remaining tanks are at almost the same temperature as the first tank which is why we only see high heat transfer in the first one. That doesn't solve the problem but it does explain the QGI/QIB plots
EDIT 2: Whoops!! The molar flow out of the tank is wrong! I'm going to take a look at this tomorrow when I have a clear head
Last edited: