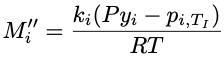- #316
casualguitar
- 503
- 26
Change madeChestermiller said:This needs to be multiplied by ##y_{in}## for CO2
To implement the integration in code, can I do a cumulative sum here like this:Chestermiller said:This assumes that the mass balance is truly satisfied. The objective of this exercise is to check to see if that is the case. If ##\dot{m}_i(t)## is the total molar flow rate out of tank i at time t, then the total molar amount of CO2 leaving the column up to time t is$$\int_0^t{\dot{m}_n(t')y_{CO2}(t')dt'}$$
$$\int_0^t{\dot{m}_n(t')y_{CO2}(t')dt'} = \sum_{t=0}^t{\dot{m}_{out}y_{CO2,OUT}}$$
which is just calculating the outlet CO2 flow at all times and summing them together
Change madeChestermiller said:The total molar holdup of CO2 in the gas would be $$M_{CO2} = \sum_{j=1}^{n}(P/RT_j)y_{j,CO2}(A_cdz*\epsilon)\tag{4}$$
Note that the summation is from tank 1 to tank n, the mole fraction of CO2 multiplies the total number of moles, and that you multiply by the void fraction rather than dividing.
In regards to defining the 'fraction of CO2 captured up to a given time'. So we agreed that 'captured' means 'in the solid phase', but what is this a fraction of?Chestermiller said:I don't know what this means, but it doesn't sound correct.
I was thinking:
Fraction of CO_2 captured = ##\frac{M_{CO2,SOLID}}{M_{CO2,SOLID} + M_{CO2,GAS}}## at a given time, which is the moles of CO2 divided by the total mass of CO2 in the packed bed, at a given time
What this definition doesn't capture is the 'fraction of CO2 captured ##\textbf{up to a given time}##. The above definition can only calculate the fraction of CO2 captured ##\textbf{at to a given time}##, so I guess my definition above isn't correct, unless you meant at a given time rather than up to a given time?
I'll post those changed plots once the simulation finishes